poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
ik heb alle dubbellingen verwijdert en een kleine bug gerepareerd en dit zijn de resultaten:
eerste n priemgetallen--------combinaties---------uitzonderingen
8 (<20)-------------------120------------------11
12 (<40)-------------------364------------------12
17 (<60)-------------------969------------------12
22 (<80)-------------------2024-----------------12
25 (<100)------------------2925-----------------12
het lijkt erop alsof de volgende 12 getallen de enige uitzonderingen zijn:
8(2*2*2),12(2*2*3),18(3*3*2),20(5*2*2),30(5*2*3),42(7*2*3),70(7*5*2),66(2*3*11),78(2*3*13),102(2*3*17),114(2*3*19) en 138(2*3*23)
na nog wat testen lijkt het alsof 4(2*2),6(2*3),10(2*5) en 14(2*7) de enige uitzonderingen zijn bij 2 priemfactoren.
eerste n priemgetallen--------combinaties---------uitzonderingen
8 (<20)-------------------120------------------11
12 (<40)-------------------364------------------12
17 (<60)-------------------969------------------12
22 (<80)-------------------2024-----------------12
25 (<100)------------------2925-----------------12
het lijkt erop alsof de volgende 12 getallen de enige uitzonderingen zijn:
8(2*2*2),12(2*2*3),18(3*3*2),20(5*2*2),30(5*2*3),42(7*2*3),70(7*5*2),66(2*3*11),78(2*3*13),102(2*3*17),114(2*3*19) en 138(2*3*23)
na nog wat testen lijkt het alsof 4(2*2),6(2*3),10(2*5) en 14(2*7) de enige uitzonderingen zijn bij 2 priemfactoren.
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
En je test hier dat
Toch? Zo ja, heb je voor je voorbeelden een a gevonden zodat de ongelijkheid niet opgaat?Mastrem schreef:
dat we dan moeten bewijzen dat voor elke
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
a is altijd een priemgetal of een macht daarvan. het is niet precies de manier hoe ik ze gevonden heb, maar ja dat is zo.
2 priemfactoren werkt niet voor 4,6,10 en 14 en alles met 3 priemfactoren wat niet werkt is deelbaar door 4 of 6, zou misschien betekenen dat als:
}{f(n)}<\frac{a}{a-1})
dat de ongelijkheid voor n dan ook niet werkt.
2 priemfactoren werkt niet voor 4,6,10 en 14 en alles met 3 priemfactoren wat niet werkt is deelbaar door 4 of 6, zou misschien betekenen dat als:
dat de ongelijkheid voor n dan ook niet werkt.
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
Okay. Maar in je ongelijkheid is a een exponent. Waarom beperk je die tot een priemgetal of een macht daarvan?
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
oeps, rechterlid had 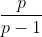 moeten zijn...
moeten zijn...
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
Maar a is dan nog steeds een exponent in de ongelijkheid.Mastrem schreef:a is altijd een priemgetal of een macht daarvan.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
oke, ik was net even afgeleid, het moet dit zijn: a is een natuurlijk getal, p een priemgetal.
als=\frac{e^{H_n}*ln(H_n)}{n})
dan zouden we kunnen bewijzen dat:
}{f(n)}\geq\frac{p}{p-1})
voor de meeste getallen dan (vermoeden: als de ongelijkheid werkt voor n en werkt dit ook)
werkt dit ook)
als
dan zouden we kunnen bewijzen dat:
voor de meeste getallen dan (vermoeden: als de ongelijkheid werkt voor n en
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
En n is een natuurlijk getal? Misschien kan je a wegwerker door ) en
en ) te onderzoeken. Als
te onderzoeken. Als  \ge f(pn)) dan hoef je alleen nog
dan hoef je alleen nog }{f(n)} \ge \frac{p}{p-1}) te onderzoeken.
te onderzoeken.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
ja, n is een natuurlijk getal.
een goed idee om a zo weg te werken! Het zou betekenen dat als}{f(n)}\geq\frac{p}{p-1}) , dat dan geldt voor elke natuurlijke
, dat dan geldt voor elke natuurlijke 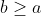 :
:
}{f(n)}\geq\frac{p}{p-1})
zo zou je met n=1 al kunnen bewijzen dat de originele vergelijking klopt voor elke macht van elk priemgetal
=1) dus je hoeft alleen maar de laagste macht van een priemgetal te vinden wat werkt.
dus je hoeft alleen maar de laagste macht van een priemgetal te vinden wat werkt.
volgens mij kunnun we zeggen dat omdat}{p^a}\sim\frac{p}{p-1}) dat als
dat als \geq\frac{p_n}{p_n-1}) , dat dan voor elke m > n
, dat dan voor elke m > n
\geq\frac{p_m}{p_m-1})
we vinden dat 5 het eerste priemgetal is waarvoor\geq\frac{p}{p-1})
dit bewijst volgens mij dat de ongelijkheid klopt voor elke macht van elk priemgetal groter dan 3.
een goed idee om a zo weg te werken! Het zou betekenen dat als
zo zou je met n=1 al kunnen bewijzen dat de originele vergelijking klopt voor elke macht van elk priemgetal
volgens mij kunnun we zeggen dat omdat
we vinden dat 5 het eerste priemgetal is waarvoor
dit bewijst volgens mij dat de ongelijkheid klopt voor elke macht van elk priemgetal groter dan 3.
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
na wat testen ben ik erachter gekomen dat 2^4 en 3^2 de laagste machten van respectievelijk 2 en 3 zijn waarvoor geldt
\geq\frac{p}{p-1})
2,3,4 en 8 kunnen simpel getest worden en dus bewijst dit volgens mij dat de ongelijkheid klopt voor alle machten van alle priemgetallen.
2,3,4 en 8 kunnen simpel getest worden en dus bewijst dit volgens mij dat de ongelijkheid klopt voor alle machten van alle priemgetallen.
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
f(1) = 0, dus hoe kan je iets zeggen over f(n) in de noemer met n = 1?
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
oja, nou dan nemen de orinele functie
=H_n+e^{H_n}*ln(H_n))
dat werkt wel
(ik had moeten zeggen dat ik f(n) veranderd had)
dat werkt wel
(ik had moeten zeggen dat ik f(n) veranderd had)
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
Je had f(n) nog eens genoemd. Maar je kan de ongelijkheid onderzoeken voor n > 1 en welke functie f ook. Dan moet je wel de gevolgen bekijken voor n = 1, en wat het onderzoek naar f bewijst voor n > 1.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
okay, maar ik heb nu toch duidelijk gemaakt dat je kan delen door f(1)? volgens mij klopt mijn bewijs dat de ongelijkheid klopt voor alle machten van elk priemgetal nu gewoon.
oh, ik heb in mijn bewijs staan=1) , dat moet natuurlijk
, dat moet natuurlijk =1) zijn
zijn
oh, ik heb in mijn bewijs staan
Re: poging Hn+e^Hn*ln(Hn)>=delersom(n) te bewijzen
Hoeft je bewijs niet meer te worden geüpdatet voor de nieuwe f? Bijv. eerste priemgetal waarvoor het geldt? Of blijft dat alles hetzelfde?
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)

