Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Matrixrekenen, vectorruimten, groep-en ringstructuren, (lineaire) tranformaties.
-
Johannes
- Vast lid

- Berichten: 63
- Lid geworden op: 19 mar 2011, 15:32
Bericht
door Johannes » 13 okt 2011, 22:38
Beste allemaal,
Ik ben bezig met het doorwerken van het basisboek van Jan van de Craats en ik kwam op een voor mij nieuw begrip. Het gaat hier over het inwendig product. Ik kan de rekenopgaven wel maken, maar het begrip blijft voor mij vaag..
Stel

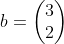
dan is het inwendig product gelijk aan
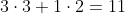
Maar wat moet ik me bij dit getal nu voorstellen?
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 14 okt 2011, 13:04
Het inwendig product krijgt betekenis in de formule voor de hoek tussen twee vectoren.
Bereken in jouw vb eens de hoek tussen deze twee vectoren.
Welke werkwijzen volg je?
-
Johannes
- Vast lid

- Berichten: 63
- Lid geworden op: 19 mar 2011, 15:32
Bericht
door Johannes » 14 okt 2011, 16:25
)
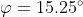
Waarbij ik de lengte van de vectoren heb uitgerekend met Pythagoras.
Ik heb me nog nooit in goniometrie hoeven te verdiepen, dus misschien ligt het daaraan dat ik het niet helemaal begrijp..
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 15 okt 2011, 14:29
Ok, nu staat er:
Johannes schreef:=\frac{(\underline{a},\underline{b})}{|\underline{a}||\underline{b}|})
En daar heb je de (meetkundige) betekenis van het inwendig product.
Zie je kans die formule te bewijzen?
Opm: nu ken ik de notatie die jullie voor het inwendig product gebruiken niet ...
-
Johannes
- Vast lid

- Berichten: 63
- Lid geworden op: 19 mar 2011, 15:32
Bericht
door Johannes » 16 okt 2011, 20:11
Ik zou niet weten hoe ik daar aan moet beginnen, maar als ik logisch nadenk: Cosinus gebruik je als je de overstaande zijde hebt gedeeld door de aanliggende. Maar dan heb je toch ook een hoek van 90graden nodig?
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 16 okt 2011, 20:15
Ga uit van twee vectoren a en b en pas de cos-regel toe in drh OAB voor hoek <AOB.
-
David
- Moderator

- Berichten: 4927
- Lid geworden op: 14 mei 2009, 16:22
Bericht
door David » 17 okt 2011, 10:13
Johannes schreef:Cosinus gebruik je als je de overstaande zijde hebt gedeeld door de aanliggende.
Klopt dat voor een gelijkbenige rechthoek abc met ab = bc = 1 en ac = sqrt(2)?
Een ezelsbruggetje is soscastoa.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
-
Johannes
- Vast lid

- Berichten: 63
- Lid geworden op: 19 mar 2011, 15:32
Bericht
door Johannes » 18 okt 2011, 09:42
SafeX schreef:Ga uit van twee vectoren a en b en pas de cos-regel toe in drh OAB voor hoek <AOB.
(Maar als ik die twee vectoren teken vanuit de oorsprong dan heb ik toch geen hoek van 90 graden ergens? Hoe pas ik dan de cos-regel toe?) Excuus,ik ga mij eerst even verdiepen in de cos-regel.
David schreef:Johannes schreef:Cosinus gebruik je als je de overstaande zijde hebt gedeeld door de aanliggende.
Klopt dat voor een gelijkbenige rechthoek abc met ab = bc = 1 en ac = sqrt(2)?
Een ezelsbruggetje is soscastoa.
Ja, dan krijg je twee hoeken van 45graden.
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 18 okt 2011, 10:03
Excuus,ik ga mij eerst even verdiepen in de cos-regel.
Dat is basiskennis ... , evenals de sin-regel.

