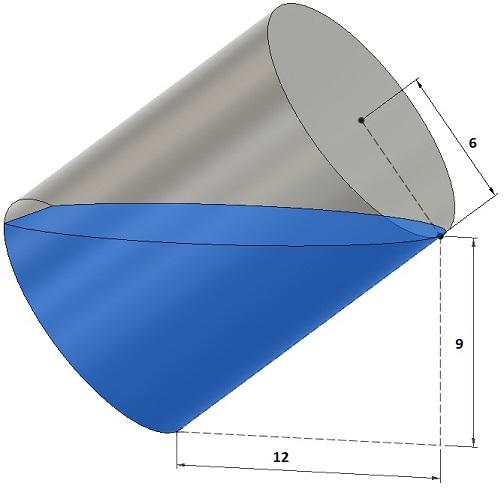
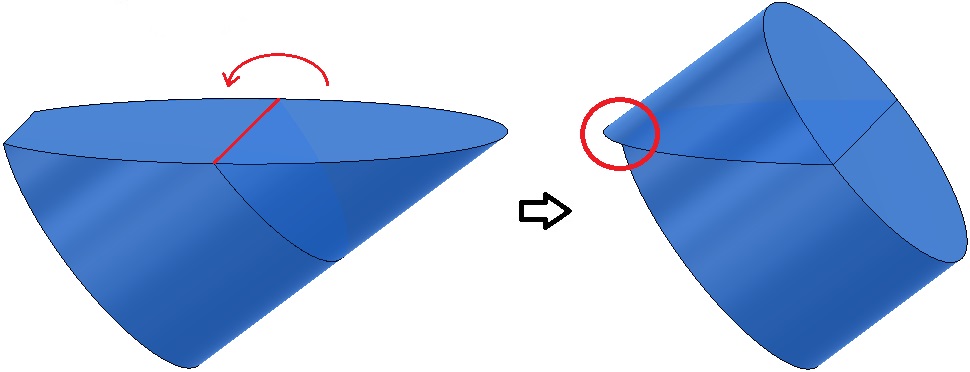
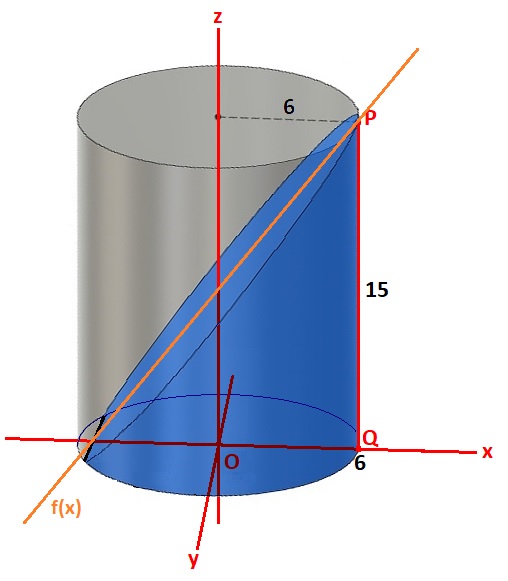
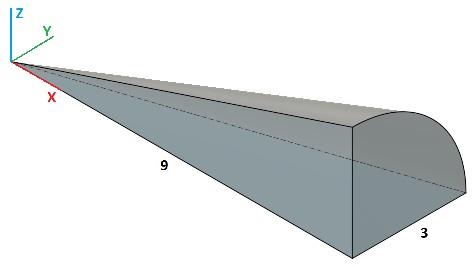
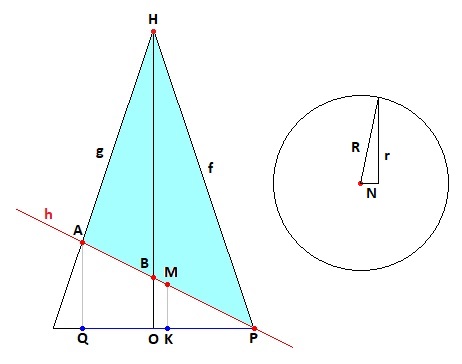
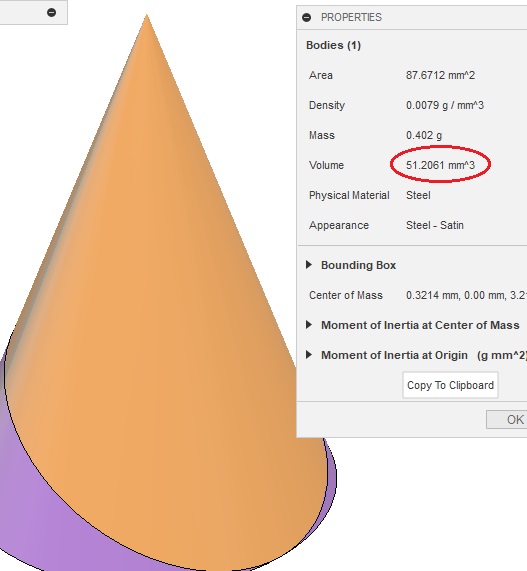
Om te beginnen: ... de vergelijking van de rechte uit onderstaande afbeelding.
In figuur (b) is de formule voor het bovenvlak:
\(V: \;z = f(x, y)=\frac{4x}{3}+7\)
Jouw lijn
\(f(x)=\frac{4x}{3}+7\) is de doorsnede van V met het vlak
\(y = 0\) (= het vlak opgespannen door de x-as en de z-as).
Deze twee functievoorschriften zijn hetzelfde omdat de y-as parallel loopt aan V, maar we werken hier met het hele bovenvlak als begrenzing van het water (dus overal de begrenzing naar boven, afhankelijk van een gegeven x en y).
... ik vermoed dat de 1 in jou formule moet vervangen worden door ...
Als onder- en bovengrens voor x vind ik -5.25 en 6.
De bovengrens voor z lijkt mij 15 te zijn.
Losjes gezegd:
Voor elk klein vierkantje
\(dx \times dy\) in het grondvlak (= x-y vlak) kijken we naar de hoogte van de kolom (= z = f(x, y)), uitgedrukt in eenheden dz. De drievoudige integraal sommeert (telt) het aantal kubusjes, elk met inhoud
\(dx \times dy \times dz\).
Zouden we overal de maximale waarde voor z op 15 stellen, dan sommeer je elk van de kolommen van z=0 tot z=15, dus overal over de volledige hoogte van het blikje, en dat is niet onze bedoeling.
De 1 komt van 1 volume-eenheid
\(dx \times dy \times dz\), en de sommatie telt hoeveel van die kubusjes er zijn. De integraal bepaalt zo het totale volume: het aantal eenheden
\(\times\) het volume van elke eenheid.
Dit levert voor dit probleem:
\(\displaystyle W = \int_{x=-5.25}^6 \int_{y=-\sqrt{36-x^2}}^\sqrt{36-x^2} \int_{z=0}^{\frac{4}{3}x + 7} 1 \;dz\;dy\;dx\)
We werken eerst de binnenste integraal uit. De primitieve van 1 naar z is z:
\(\displaystyle W = \int_{x=-5.25}^6 \int_{y=-\sqrt{36-x^2}}^\sqrt{36-x^2} \begin{bmatrix} z \end{bmatrix}_0^{\frac{4}{3}x + 7} \;dy\;dx\)
vervolgens vullen we de grenzen in:
\(\displaystyle W = \int_{x=-5.25}^6 \int_{y=-\sqrt{36-x^2}}^\sqrt{36-x^2} \left(\frac{4}{3}x + 7 - 0\right) \;dy\;dx\)
En dit ziet er waarschijnlijk al wat bekender uit: hier staat:
"voor x binnen de gegeven grenzen sommeren we (voor y binnen de gegeven grenzen sommeren we (deze functie van x en y))"
Merk op: dit is nog steeds een functie van x en y, alleen vanuit y bezien is het hier een constante functie (er komt geen y voor in het functievoorschrift).
Voor y geldt een soortgelijk verhaal als voor z hierboven: als we y zouden laten lopen van -6 tot 6, dan krijgen we als grondvlak geen cirkel, maar een rechthoek, begrensd door y=-6 en y=6.
De correcte begrenzing van y wordt gegeven door een cirkel (= het grondvlak van het blikje),
de waarde van deze grenzen kunnen we voor elke gegeven x berekenen uit de cirkelformule :
\(y_{min/max} = \pm \sqrt{r^2 - x^2}\) (waarbij r = de straal van de cirkel).
In een plaatje:

op elk vierkantje staat een waterkolom met hoogte z = f(x, y),
De drievoudige integraal levert de sommatie voor al die volumina.
We hadden al gezien dat de integrand een constante functie is gezien vanuit y,
dus de primitieve is diezelfde constante maal y:
\(\displaystyle W = \int_{x=-5.25}^6 \left[\left(\frac{4}{3}x + 7\right)\cdot y \right]_{y=-\sqrt{36-x^2}}^\sqrt{36-x^2} \;dx\)
\(\displaystyle W = \int_{x=-5.25}^6 \left(\left(\frac{4}{3}x + 7\right)\cdot \sqrt{36-x^2} \;\;-\;\; \left(\frac{4}{3}x + 7\right)\cdot \left(-\sqrt{36-x^2}\right) \right) \;dx\)
\(\displaystyle W = \int_{x=-5.25}^6 \left( 2\cdot\left(\frac{4}{3}x + 7\right)\cdot \sqrt{36-x^2}\right) \;dx\)
\(\displaystyle W = \int_{x=-5.25}^6 \left( \frac{8}{3}x\cdot \sqrt{36-x^2} + 14\cdot \sqrt{36-x^2}\right) \;dx\)
En nu houden we een enkelvoudige integraal in x over, die we met geschikte substituties kunnen oplossen.
hoe krijg ik spaties tussen dz, dy en dx in bovenstaande formule?
In LaTeX is een spatie de twee karakter combinatie \;
Noot: je kan met je rechter muisknop op een formule klikken, kies dan in het pop-up menu "Show Math As:" en vervolgens "TeX Commands", dan krijg je de betreffende regel in LaTeX code.