radius bepalen van cirkel met 2 snijpunten schuine lijn

[CTP]

Hallo, zie onderstaande afbeelding

waarden a t/m e zijn bekend.

(In het geval van het schetsje a=5, b=3, c=4, d=15 en e=1)

Wat is de radius R?

groet,

Lucas

[arie]

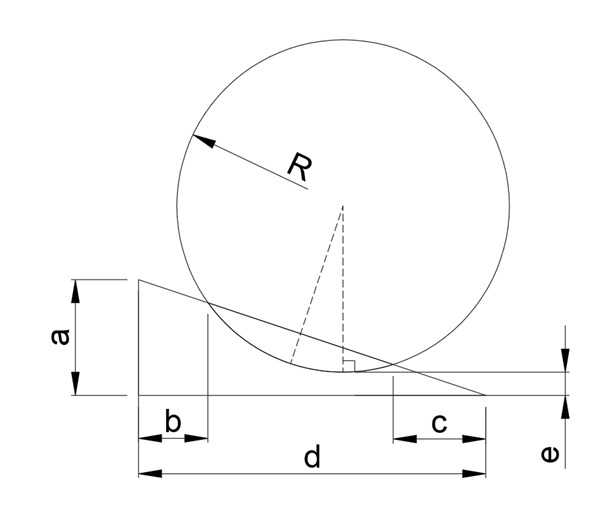
Maak een assenstelsel waarin A=(0, 5) en D=(15, 0).
Dan zijn de snijpunten van AD met de cirkel B=(3, 4) en C=(11, 4/3).
Het middelpunt M=(mx, my) ligt op de middelloodlijn (blauw) van BC:
deze loopt door P=(B+C)/2 = (7, 8/3) en heeft een richtingscoefficient van 3,
daaruit volgt als vergelijking van deze lijn:
y = 3x - 55/3
ofwel M voldoet aan:
mx = my/3 + 55/9
Noem Q=(mx, 1), dan geldt ook:
R = BM = MQ:
waardoor:
\(\sqrt{(m_x-3)^2+(m_y-4)^2} = m_y-1\)
ofwel
\(\left(\left(\frac{m_y}{3} + \frac{55}{9}\right)-3\right)^2+(m_y-4)^2 = (m_y-1)^2\)
Hieruit volgt via de abc-formule:
\(m_y = \frac{53}{3} \pm 3\sqrt{10}\)
en
\(R = m_y -1 = \frac{50}{3} \pm 3\sqrt{10}\)
Wil je dat Bx < Qx < Cx, dan is dit de oplossing:
\(R = \frac{50}{3} - 3\sqrt{10}\approx 7.1798336861615...\)
(voor de andere oplossing geldt Qx > Cx)

[CTP]

top!

Ik zat me er helemaal blind op te staren.

klopt helemaal

dank je!