Ik zit hier met een vraagstuk waarvoor ik de oplossing niet voor mij kan zien. Ik heb x identieke balletjes die willekeurig verdeeld kunnen worden over N bakjes. Niet in elk bakje hoeft een balletje te zitten. Op hoeveel verschillende manier kan ik de balletjes verdelen? (voor een gegeven x en N).
Is er een algemene oplossing hiervoor?
X Identieke balletjes verdelen over N bakjes
-
LifeLongLearner
- Nieuw lid

- Berichten: 6
- Lid geworden op: 07 feb 2013, 17:19
Re: X Identieke balletjes verdelen over N bakjes
Ja, het aantal combinaties met herhaling ...LifeLongLearner schreef:Is er een algemene oplossing hiervoor?
Re: X Identieke balletjes verdelen over N bakjes
Het antwoord ligt niet echt voor de hand. Er is een trucje voor nodig. Ik ga het niet verklappen maar ik zet je op weg:
Stel je hebt 6 balletjes en 3 doosjes: A, B en C.
Teken eerst de balletjes die in doos A gaan, dan diegene die in B gaan en daarna die van C.
Een mogelijke verdeling is dan bijvoorbeeld:
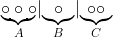 .
.
Wat is nu het totaal aantal manieren denk je?
Stel je hebt 6 balletjes en 3 doosjes: A, B en C.
Teken eerst de balletjes die in doos A gaan, dan diegene die in B gaan en daarna die van C.
Een mogelijke verdeling is dan bijvoorbeeld:
Wat is nu het totaal aantal manieren denk je?
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.
Re: X Identieke balletjes verdelen over N bakjes
stel er zijn 10 identieke balletjes en je verdeelt ze over 4 verschillende dozen
Oplossing:
je neemt 10 uit 4 (je gaat 10 keer kiezen uit 4 dozen, elk balletje kan in 1 van de 4 dozen terecht komen)
hierbij is herhaling mogelijk aangezien je meerdere keren kan kiezen om je balletje bijvoorbeeld in doos 1 te leggen
hierbij is volgorde niet belangrijk, of je nu eerst een balletje in de eerste doos legt en daarna is de tweede doos of omgekeerd, dit maakt niet uit aangezien alle balletjes gelijk zijn (dit zou anders zijn als de balletjes bijvoorbeeld genummerd waren of elk een ander kleur hadden)
besluit: 10 uit 4, herhaling mag, volgorde niet van belang
dit is een herhalingscombinatie van 10 uit 4
een herhalingscombinatie van p uit n is gelijk aan de combinatie van p uit p+n-1, in ons geval is de herhalingscombinatie van 10 uit 4 dus gelijk aan de combinatie van 10 uit 13
de combinatie van 10 uit 13 = (13!)/(10! * 3!) = 286 mogelijkheden om 10 identieke balletjes over 4 verschillende dozen te verdelen
Oplossing:
je neemt 10 uit 4 (je gaat 10 keer kiezen uit 4 dozen, elk balletje kan in 1 van de 4 dozen terecht komen)
hierbij is herhaling mogelijk aangezien je meerdere keren kan kiezen om je balletje bijvoorbeeld in doos 1 te leggen
hierbij is volgorde niet belangrijk, of je nu eerst een balletje in de eerste doos legt en daarna is de tweede doos of omgekeerd, dit maakt niet uit aangezien alle balletjes gelijk zijn (dit zou anders zijn als de balletjes bijvoorbeeld genummerd waren of elk een ander kleur hadden)
besluit: 10 uit 4, herhaling mag, volgorde niet van belang
dit is een herhalingscombinatie van 10 uit 4
een herhalingscombinatie van p uit n is gelijk aan de combinatie van p uit p+n-1, in ons geval is de herhalingscombinatie van 10 uit 4 dus gelijk aan de combinatie van 10 uit 13
de combinatie van 10 uit 13 = (13!)/(10! * 3!) = 286 mogelijkheden om 10 identieke balletjes over 4 verschillende dozen te verdelen


