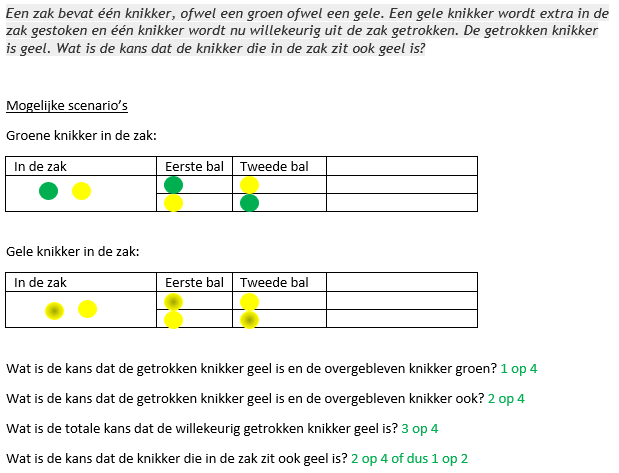
Een zak bevat één knikker, ofwel een groen ofwel een gele. Een gele knikker wordt extra in de zak gestoken en één knikker wordt nu willekeurig uit de zak getrokken. De getrokken knikker is geel. Wat is de kans dat de knikker die in de zak zit ook geel is?
Speel je hier met 2 (1 geel of groen en geel) of 3 knikkers (2 geel en 1 groen)? Hoe moet je beginnen aan een kansboom als je maar met 2 knikkers speelt? Ik weet niet hoe ik aan deze oefening moet beginnen.
Alvast bedankt voor een tip.
Onbekende knikker
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Onbekende knikker
In het begin zit er 1 knikker in de zak die groen of geel is. Er wordt vervolgens 1 gele knikker in de zak bijgestopt. Je trekt nu willekeurig 1 knikker uit de zak. Wat is de kans dat de getrokken knikker geel is en de overgebleven knikker groen? Wat is de kans dat de getrokken knikker geel is en de overgebleven knikker ook? Wat is dus de totale kans dat de willekeurig getrokken knikker geel is?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Onbekende knikker
Ik kom niet verder dan 1 op 2.
Zie bijlage.
Zie bijlage.
Re: Onbekende knikker
In het plaatje staan 4 scenario's die ZONDER VOORKENNIS alle 4 even waarschijnlijk zijn:
scenario 1: 1=groen, 2=geel
scenario 2: 1=geel, 2=groen
scenario 3: 1=geel, 2=geel
scenario 4: 1=geel, 2=geel
Nu wordt er gezegd dat de eerste knikker geel is.
Dan houden we 3 mogelijkheden over (scenario 2 t/m 4) die alle 3 nog steeds even waarschijnlijk zijn.
Wat is nu de kans dat de tweede knikker geel is?
In feite is dit vergelijkbaar met het volgende probleem:
Gegeven: in een zak zit 1 knikker: een groene, gele, rode of blauwe knikker, elk met kans 1/4.
Nu wordt bekend gemaakt dat de knikker in de zak NIET blauw is.
Er blijven dan ook 3 mogelijke situaties over.
Wat is nu de kans dat er een rode knikker in de zak zit?
Door het extra gegeven (= de extra kennis) veranderen in beide gevallen de kansen op de overgebleven scenario's.
scenario 1: 1=groen, 2=geel
scenario 2: 1=geel, 2=groen
scenario 3: 1=geel, 2=geel
scenario 4: 1=geel, 2=geel
Nu wordt er gezegd dat de eerste knikker geel is.
Dan houden we 3 mogelijkheden over (scenario 2 t/m 4) die alle 3 nog steeds even waarschijnlijk zijn.
Wat is nu de kans dat de tweede knikker geel is?
In feite is dit vergelijkbaar met het volgende probleem:
Gegeven: in een zak zit 1 knikker: een groene, gele, rode of blauwe knikker, elk met kans 1/4.
Nu wordt bekend gemaakt dat de knikker in de zak NIET blauw is.
Er blijven dan ook 3 mogelijke situaties over.
Wat is nu de kans dat er een rode knikker in de zak zit?
Door het extra gegeven (= de extra kennis) veranderen in beide gevallen de kansen op de overgebleven scenario's.
Re: Onbekende knikker
Doordat het aantal gunstige uitkomsten gelijk blijft maar het aantal mogelijke uitkomsten verkleind wordt de kans groter.
De teller blijft gelijk, de noemer wordt kleiner dus resultaat wordt groter.
De kans dat de knikker in de zak nog geel is, is 2 op 3.
De teller blijft gelijk, de noemer wordt kleiner dus resultaat wordt groter.
De kans dat de knikker in de zak nog geel is, is 2 op 3.
Re: Onbekende knikker
OK, correct.